Wavelength
Wavelength
When radio was young, wavelength was the characteristic which differentiated stations from one another (see the tuning dial to the right). This physics notion underlies the expression "Being on the same wavelength", thinking the same thing.
The concept of wavelength, an alternate representation of frequency, is useful in calculating the length of antennas: antennas are frequently fractions of the wavelength, such as ¼ or ½.
- Electromagnetic waves travel at 300 000 kilometres / second (in a vacuum), i.e., the speed of light.
- [ In imperial units, this speed is known as 186 000 miles per second. ]
- Wavelength ( symbol: λ, lowercase Greek letter lambda ) may be defined as follows:
- Distance travelled during one cycle, or
- Distance separating two similar points on the wave ( e.g., two crests ).
- Wavelength is computed as "distance travelled in one second" divided by "number of cycles in that second":
- λ in metres = 300 000 000 m/s ÷ frequency in hertz.
- Millions of metres and millions of cycles cancel one another and yield this simplified formula: λ in metres = 300 ÷ f in MHz.
- [ In imperial units, the simplified formula reads: λ in feet = 984 ÷ f in MHz. ]
- Wavelength and frequency have a reciprocal relation:
- When wavelength shortens, frequency increases.
- When frequency decreases, wavelength lengthens.
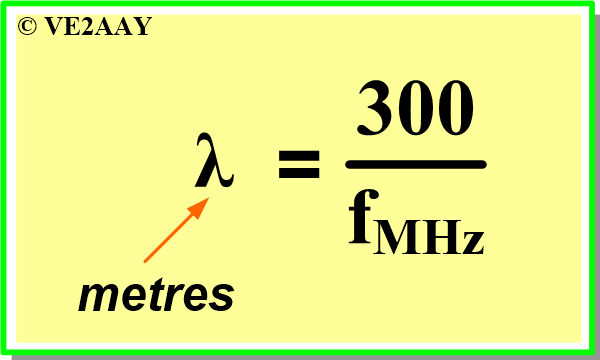
Sample calculation
Wavelength at 1875 kHz = 300 / 1.875 MHz = 160 metres.
Suggestion:
The metric system really simplifies wavelength and antenna calculations: i.e., the connection between 300 000 km/s (speed of light) and "magic" number 300 is more easily memorized than the pair of 186 000 mi/s and 984!
Exercises
Some training before hitting the Question Bank
Click on a question to view the answer …
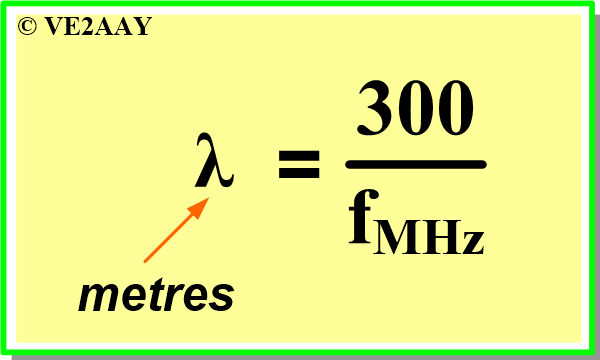
To learn more: Wikipedia article on speed of light (new tab or window) and Wikipedia article on wavelength (new tab or window).
\

